A térről általában
Mi a TÉR?
A TÉR egy elvonatkoztatás: - zárt és nyitott térrészek összessége. (1. megközelítés)
- pontok összessége. (2. megközelítés)
Mi jellemzi a teret?
HA térben akarunk tájékozódni, vagyis azt szeretnénk tudni, hogy mi hol van, akkor A TÉR PONTOKBÓL (virtuális, kiterjedés nélküli összetevőkből) ÁLL!
+ (Tudjuk még, hogy) A TÉR pontjait számok segítségével azonosítani lehet.
↓ (Ebből az következik, hogy)
A tér valójában a térbeli koordináta rendszer pontjainak összessége.

(No, de!) A térbeli koordináta rendszer három egymásra merőleges, jobbsodrású koordinátatengelyből áll (x,y,z). (1. ábra)
Bármely pont helyét egyértelműen meg tudjuk határozni ebben a rendszerben a három koordinátájával:
x = abszcissza,
y = ordináta,
z = applikáta.
Ezt a rendszert
- az origója
- az x irányú egységpontja
- az y irányú egységpontja
- a z irányú egységpontja egyértelműen meghatározza.
Ez a négy pont nem illeszkedik egy síkra (nem komplanáris).
(Vagyis ebben az esetben jellemzően 3 távolság segítségével adjuk meg a pont helyzetét.)
Használatos még ugyanakkor:
- hengerkoordináta rendszer: két távolság és egy szög segítségével adjuk meg a pont helyzetét.
- gömbi koordináta rendszer: egy távolság és két szög segítségével adjuk meg a pont helyzetét. (lásd földrajzi helymeghatározás)

Ha a (valódi, azaz kiterjedéssel rendelkező) téralkotókat akarjuk jellemezni, mi milyen alakú, mekkora kiterjedésű, akkor
a koordináta rendszerre nem lesz szükségünk. (Hurrá!)
Hány dimenziós a tér?
A tér matematikában mindig 3 dimenziós. Minden zárt térbeli alakzatnak van:
- hosszúsága (maximális x irányú kiterjedése)
- szélessége (maximális y irányú kiterjedése)
- magassága (maximális z irányú kiterjedése)
A kiterjedést úgy kapjuk, hogy belefoglaljuk képzeletben az adott testet egy olyan téglalapba, amelynek az élei párhuzamosak a tengelyekkel.

A modern matematika és a modern fizika kiterjesztette a dimenzió fogalmát.
Az egyik legszebb kiterjesztés a fraktáloké, amelyek törtdimenziós alakzatok és főként a káoszelméletben használatosak.
A háromnál több dimenziós alakzatokkal nem foglalkozunk. (Hurrá!)

Mi a kubizmus?
A kubizmus az az avantgard (modernista) festészeti stílusirányzat,
amely azt ténylegesen is megjeleníti a a környezet dolgainak a mértani alakzatokra való felbontását. Leghíresebb képviselője Picasso volt.

Van-e a térnek görbülete?
Euklidész szerint a térnek nincs görbülete: - a párhuzamos egyenesek nem találkoznak.
- egy háromszög szögeinek összege 180°.
A nem Euklidészi geometriák (Bolyai-Lobacsevszkij-Riemann) szerint a térnek van görbülete:
- a párhuzamosak találkoznak.
- a háromszögek (pl. gömbháromszög) belső szögeinek összege nem 180°.
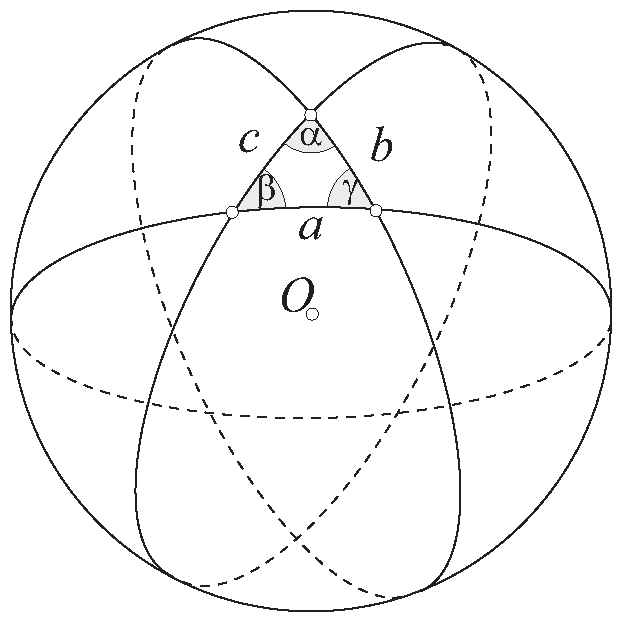
Mi a nem Euklidészi geometriákkal nem foglalkozunk. (Hurrá!)
Gondolattérkép:
Ellenőrző kérdések:
1. Mikor fogjuk fel a teret ponthalmazként? 2. Miben tér el a térbeli és a síkbeli koordináta rendszer egymástól?
3. Milyen térbeli koordináta rendszereket használnak leggyakrabban?
4. Mit jelent az a szó, hogy kollineáris és mit jelent az, hogy komplanáris?
5. Hogy hívják a -Descartes-féle térbeli koordináta rendszerben a tengelyeket?
6. Mit jelent az, hogy a térbeli testek 3 dimenziósak?
7. Milyen kapcsolat van Picasso és a geometria között?
8. Milyen térbeli alakzatok a testek, nyitottak vagy zártak?
9. Mit mondott Euklidész a tér görbületéről?
10. Kik voltak az Euklideszi geometria mindenhatóságának megkérdőjelezői?