KIDOLGOZOTT FELADAT
Hétköznapi tárgyakkal (golyókkal, kavicsokkal, pálcikákkal, lapokkal, dobozokkal stb.) készíts modellt a feladat szövegének megfelelően!Mutasd meg, mondd el részletesen társaidnak a megoldásra vonatkozó ötleteidet!
1. Négy hajó úgy helyezkedik el, hogy bármelyik kettő egymástól 40 méter távolságra van.
A négy közül három vitorlás.
Milyen hajó lehet a negyedik?
(A hajókat pontszerűnek tekintjük.)
A négy közül három vitorlás.
Milyen hajó lehet a negyedik?
(A hajókat pontszerűnek tekintjük.)
2. Egy pók a szoba egyik sarkából a tőle legtávolabbi sarokba szeretne eljutni.
A téglatest alakú helyiség szélessége 2 méter, hosszúsága 4 méter, és magassága 2,5 méter.
a) Mekkora a legrövidebb út, ha a pók bárhol, akár a levegőben kifeszített fonálon is haladhat?
b) Mekkora a legrövidebb út, ha a pók csak az oldalfalakon, a plafonon és a padlón mászva tud haladni?
A téglatest alakú helyiség szélessége 2 méter, hosszúsága 4 méter, és magassága 2,5 méter.
a) Mekkora a legrövidebb út, ha a pók bárhol, akár a levegőben kifeszített fonálon is haladhat?
b) Mekkora a legrövidebb út, ha a pók csak az oldalfalakon, a plafonon és a padlón mászva tud haladni?
ELMÉLET
Térelemek: pont, egyenes, sík, tér.Térelemek kölcsönös helyzete
Két egyenes metsző, ha pontosan egy közös pontjuk van.Két egyenes párhuzamos, ha egy síkban vannak, és nincs közös pontjuk (vagy ha egybeesnek).
Két egyenes kitérő, ha nincs olyan sík, amelyre mindkét egyenes illeszkedik.
Egy egyenes illeszkedik egy síkra, ha minden pontja a síkon van.
Egy egyenes metsz egy síkot, ha pontosan egy közös pontjuk van.
Egy egyenes párhuzamos egy síkkal, ha nincs közös pontjuk (vagy ha illeszkedik rá).
Két különböző sík metszi egymást, ha a két síknak van közös pontja.
A közös pontok által alkotott egyenes a két sík metszésvonala.
Két sík párhuzamos, ha nincs közös pontjuk (vagy ha egybeesnek).
Térelemek távolsága
Két pont távolsága a pontok által meghatározott szakasz hossza.Két ponthalmaz távolságát a ponthalmazok pontjai között mért távolságok minimuma adja.
Ha két térelemnek van közös pontja (metszik egymást, vagy illeszkednek egymásra), akkor távolságuk 0.
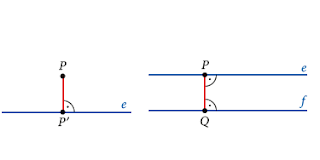
Pont és egyenes távolsága a pontból az egyenesre állított merőleges szakasz hossza.
Két párhuzamos egyenes távolsága az egyik egyenes egy tetszőleges pontjának a másik egyenestől való távolsága.
Pont és sík távolsága a pontból a síkra állított merőleges szakasz hossza.
Sík és egy vele párhuzamos egyenes távolsága az egyenes tetszőleges pontjának a síktól való távolsága.
Két párhuzamos sík távolsága az egyik sík egy tetszőleges pontjának a másik síktól való távolsága.
Lapátló, testátló:
Egy sokszöglapokkal határolt test (ún. poliéder) két csúcsát összekötő szakasz lehet a test egyik éle vagy egyik átlója.Ha egy átló illeszkedik a test valamelyik lapjára, akkor az lapátló, ha nem ugyanazon a lapon lévő csúcsokat köt össze, akkor testátló.
Megjegyzés
1. A téglatest testátlójának hossza meghatározható úgy, hogy az egy csúcsból induló élhosszak négyzetösszegének vesszük a négyzetgyökét:`color(red)(e = sqrt(a^2 + b^2 + c^2))`
2. Az a élhosszúságú kocka lapátlójának hossza `color(red)(f = a*sqrt(2))`,
testátlójának hossza `color(red)(e = a*sqrt(3)`.
FELADAT
1. Egy kocka lapátlójának hossza (e =) `sqrt(10)` egység.
Mekkora a kocka testátlójának hossza?
e = ✓ ✗
a = ✓ ✗
f = ✓ ✗
Mekkora a kocka testátlójának hossza?
e = ✓ ✗
a = ✓ ✗
f = ✓ ✗
2. Tekintsük az ABCDA'B'C'D' téglatestet (lásd az ábrát)!
Éleiről tudjuk, hogy AD = 7 m, AB = 12 m, valamint AA'= 5 m.
Milyen távolságban vannak a téglatest AD élétől a téglatest élei?
AB = AD = CD = BC =
AA' = BB' = CC' = DD' =
A'B' = A'D' = B'C' = D'C' = ✓ ✗
Éleiről tudjuk, hogy AD = 7 m, AB = 12 m, valamint AA'= 5 m.
Milyen távolságban vannak a téglatest AD élétől a téglatest élei?
AB = AD = CD = BC =
AA' = BB' = CC' = DD' =
A'B' = A'D' = B'C' = D'C' = ✓ ✗
3. Milyen távol van a kocka egyik testátlója a kocka csúcsaitól, ha a kocka élének hossza 8 cm?
e = cm ✓ ✗
f = cm ✓ ✗
T = ✓ ✗
m = cm ✓ ✗
e = cm ✓ ✗
f = cm ✓ ✗
T = ✓ ✗
m = cm ✓ ✗
4. Egy téglatest alakú terem plafonjának közepéről lelógatnak egy (h =) 40 cm = m hosszúságú zsinóron lévő, pontszerű lámpatestet.
A terem összes élhosszának összege *(a + b + c =) 53,2 méter.
A terem magasságának, szélességének és hosszának aránya ilyen sorrendben 4 : 6 : 9.
Milyen távol van a lámpatest
a) a padlótól;
*x + *x + *x =
x = m
a = m
b = m
c = m
x1 = - = m ✓ ✗
b) a legkisebb területű faltól;
x2 = /2 = m ✓ ✗
c) a leghosszabb éltől?
x3² = ² + (/2)²
x3 = m ✓ ✗
A terem összes élhosszának összege *(a + b + c =) 53,2 méter.
A terem magasságának, szélességének és hosszának aránya ilyen sorrendben 4 : 6 : 9.
Milyen távol van a lámpatest
a) a padlótól;
*x + *x + *x =
x = m
a = m
b = m
c = m
x1 = - = m ✓ ✗
b) a legkisebb területű faltól;
x2 = /2 = m ✓ ✗
c) a leghosszabb éltől?
x3² = ² + (/2)²
x3 = m ✓ ✗
HÁZI FELADAT
1. A kocka testátlójának hossza (f =) 30 egység.
Mekkora a kocka lapátlóinak hossza?
a =
e =
Mekkora a kocka lapátlóinak hossza?
a =
e =
2. (Érettségi feladat, 2007)
Egy függőlegesen álló rádióantennát magasságának (x =) 2/3 részénél négy egyenlő, egyenként (b =) 14,5 m hosszú drótkötéllel rögzítenek a talajhoz.
A rögzítési pontok a földön egy (a =) 10 m oldalhosszú négyzetet alkotnak.
a) Milyen magas az antenna?
e = m
m² + ² = ²
m = m
M = m
b) Reklámcélokra a drótkötelek közé sátorszerűen vásznakat feszítenek ki.
Mekkora ezek együttes területe?
mo² + ² = ²
mo = m
T(háromszög) = m2
T = m2
Egy függőlegesen álló rádióantennát magasságának (x =) 2/3 részénél négy egyenlő, egyenként (b =) 14,5 m hosszú drótkötéllel rögzítenek a talajhoz.
A rögzítési pontok a földön egy (a =) 10 m oldalhosszú négyzetet alkotnak.
a) Milyen magas az antenna?
e = m
m² + ² = ²
m = m
M = m
b) Reklámcélokra a drótkötelek közé sátorszerűen vásznakat feszítenek ki.
Mekkora ezek együttes területe?
mo² + ² = ²
mo = m
T(háromszög) = m2
T = m2
3. Egy téglatest alakú terem (a =) 5 m széles, (b =) 8 m hosszú és (m =) 3 m magas.
A termet úgy választják ketté, hogy a padlólap egyik átlója mentén állítanak egy függőleges falat (ez az úgynevezett átlósík).
Milyen távol van az elválasztófal a terem függőleges éleitől?
e = m
T = a*/2 = m*/2
m = m
A termet úgy választják ketté, hogy a padlólap egyik átlója mentén állítanak egy függőleges falat (ez az úgynevezett átlósík).
Milyen távol van az elválasztófal a terem függőleges éleitől?
e = m
T = a*/2 = m*/2
m = m
4. a) Egy kocka két szomszédos lapközéppontjának távolsága (x =) 21,92 cm.
Mekkorák a kocka élei?
x² = * ()²
a = cm
b) Ha a kocka lapközéppontjait összekötjük az összes szomszédos lap lapközéppontjával, akkor a kapott szakaszok egy újabb testet alkotnak.
Hány csúcsa, hány éle, hány lapja van ennek a testnek?
csúcsok száma =
élek száma =
lapok száma =
Mekkorák a kocka élei?
x² = * ()²
a = cm
b) Ha a kocka lapközéppontjait összekötjük az összes szomszédos lap lapközéppontjával, akkor a kapott szakaszok egy újabb testet alkotnak.
Hány csúcsa, hány éle, hány lapja van ennek a testnek?
csúcsok száma =
élek száma =
lapok száma =
NÉV:
Azonosító:
Eredmény: /