26. Mértani sorozatok

Forrás: https://www.tankonyvkatalogus.hu/storage/pdf/OH-MAT12TA__teljes.pdf

KIDOLGOZOTT FELADAT

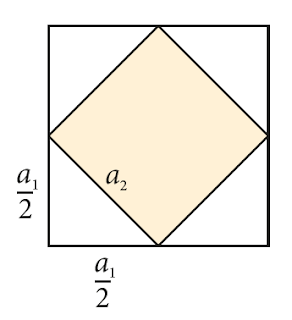
Egy 8 cm oldalhosszúságú négyzet oldalfelező pontjait sorban összekötjük.
Mivel a kapott alakzat olyan négyszög, amelyet az eredeti négyzet középpontja körüli 90°-os elforgatás önmagába visz át, ezért az oldalfelező pontok összekötésével kapott alakzat is egy négyzet.
A belső négyzet oldalfelező pontjait összekötve újabb négyzetet kapunk, és így tovább, az ábra szerint.

Ha ezt az eljárást folytatjuk, akkor mennyi
a) a negyedik négyzet kerülete és területe;
b) az n-edik négyzet kerülete és területe?

Megoldás

Az egymásba írt négyzetek hasonlók.
Mennyi a hasonlóság aránya (m) az első két négyzet esetében?

Ha az első négyzet oldalának hossza a1, és a második négyzet oldalának hossza a2, akkor Pitagorasz tétele alapján `a_2^2=(a_1/2)^2+(a_1/2)^2=2*a_1^2/4=a_1^2/2`.
Ebből: `a_2=1/sqrt(2)*a_1` és `lambda= 1/sqrt(2)` .
Megfigyelhető, hogy bármely két egymás utáni lépésben kapott négyzet esetén a hasonlóság aránya szintén `lambda = 1/sqrt(2)` .
A négyzetek oldalhosszai tehát egy olyan sorozatot alkotnak, melyben az egymás után álló tagok hányadosa állandó.
Ha a hasonlóság aránya λ, a hasonló alakzatok kerületeinek aránya is λ, a területek aránya pedig λ².
Így a négyzetek kerületei és területei is olyan sorozatot alkotnak, amelyben az egymás után álló tagok aránya állandó.
Az oldalhosszak és a kerület esetében ez a szorzószám `lambda= 1/sqrt(2)`, a területek esetében pedig `lambda^2 = 1/2` .
(Jól látható, hogy a beírt négyzet területe fele az eredeti négyzet területének.)
Az első (eredeti) négyzet oldalának hossza a1 = 8, kerülete K1 = 32, és területe T1 = 64.
(Az egységek cm, illetve cm2.)

A második négyzetre	`a_2=lambda*a_1`	`K_2=lambda*K_1`	`T_2=lambda^2*T_1`
A harmadik négyzetre	`a_3=lambda*a_2=lambda^2*a_1`	`K_3=lambda*K_2=lambda^2*K_1`	`T_3=lambda^2*T_2=lambda^4*T1`
A negyedik négyzetre	`a_4=lambda*a_3=lambda^3*a_1`	`K_4=lambda*K_3=lambda^3*K_1`	`T_4=lambda^2*T_3=lambda^6*T1`

A negyedik négyzet kerülete tehát ≈ 11,31 cm, és területe 8 cm2.
Hasonló módon, lépésről lépésre jutunk el a sorozatok n-edik tagjáig.
Az n-edik négyzetre:
`a_n=lambda^(n-1)*a_1`
`K_n=lambda^(n-1)*K_1`
`T_n=(lambda^2)^(n-1)*T_1`

FELADAT

1. Zoltán 3 millió Ft-ot helyez el a bankban, kamatos kamatra.
a) Mennyi pénze lesz ezen a számlán 6 év múlva, ha az éves kamat 3,5%?
✓ ✗
b) Mekkora az éves kamat, ha 3 840 000 Ft lesz a számláján 6 év múlva?
✓ ✗
(A kamatot évente írják jóvá. Zoltán a 6 év alatt nem nyúl ehhez a számlájához.)
//a) 3 687 766 Ft. b) 4,2%.

---

2. Egy erdő faállománya 2005 és 2020 között minden évben az elozo évhez képest 2%-kal csökkent.
2010-ben 12 000 m3 volt a faállomány.
a) Mennyi volt a faállomány 2005-ben?
✓ ✗
b) Mennyi volt a faállomány 2020-ban?
✓ ✗
c) Melyik évben csökkent a faállomány először 10 500 m3 alá?
✓ ✗
//a) 13 275 m3.
b) 9 800 m3.
c) a 7. évben.

ELMÉLET

A mértani sorozat

Definíció:

Az an sorozatot mértani sorozatnak nevezzük, ha a második tagtól kezdve bármely tag és az előtte álló tag hányadosa 0-tól különbözo állandó, vagyis n2 1 esetén a értéke állandó.
Ez az állandó a sorozat kvóciense (hányadosa).
Jele: q.

A mértani sorozat n-edik tagját (n > 1 esetén) megkapjuk, ha az előtte álló tagot megszorozzuk a kvócienssel, vagy ha az első tagot megszorozzuk a kvóciens (n - 1)-edik hatványával.
A mértani sorozatnak tehát semelyik tagja és a kvóciense sem lehet 0.

Megjegyzés:

Ha egy feladatban ismert egy mértani sorozat két tagja (és mindkettorol tudjuk, hogy hányadik tagok), akkor lehetséges, hogy a feladatnak két megoldása van.

Például:

a12 = 10; a14 = 40 → `a_14/a_12=q^2` → 4 = q² → q = 2 vagy -2.

FELADAT

3. Egy mértani sorozat első tagja 7.
Mennyi a hányados és a hatodik tag, ha a negyedik tag
a) 189
✓ ✗
b) -0,875?
✓ ✗
//a) 3 és 1701. b) -0,5 és -0,21875

---

4. Egy mértani sorozat második tagja 1600, negyedik tagja 4.
Mennyi lehet a sorozat
a) kvóciense;
✓ ✗
b) első tagja?
✓ ✗
//a) +-1/20 . b) +-32 000.

---

5. Egy mértani sorozat első tagja 8.
A második és a harmadik tag összege 16.
Mennyi lehet a sorozat negyedik tagja?
✓ ✗
✓ ✗
//8 vagy -64.

---

6. Egy vállalkozó 2021-ben vett egy 21,5 millió forint értékű gépet.
Ennek értéke évente az elozo évi értékének 15%-ával csökken.
Amikor az értékcsökkenés eléri az 55%-ot (azaz a gép értéke kevesebb lesz, mint az eredeti ár 45%-a), a gépet értékesítik, és újat vesznek helyette.
a) Mennyit ér ez a gép 3 év múlva?
(Figyelj! Ha a1 2021-es adat, akkora a választ a4 értéke adja meg!)
✓ ✗
b) Melyik évben kell értékesíteni?
✓ ✗
c) Oldd meg a b) feladatot úgy is, hogy nem használod fel a 21,5 millió forintos adatot!
✓ ✗
//13,2 millió Ft. b) 2026.

HÁZI FELADAT

1. Létezik-e olyan mértani sorozat, amelynek a táblázat egy sorában szereplő két szám a két adott sorszámú tagja?
Töltsd ki a táblázatot!
Melyik esetben nincs megoldás?
Melyik esetben van két megoldás?

	a1	a2	a3	a4	q
I.	4		-16
II.		9		81
III.	500			-864
IV.			400	-320

---

2. Egy mértani sorozat harmadik tagja 32 és hatodik tagja 108.
Hány olyan tagja van a sorozatnak, amely kisebb, mint 1 000 000?

---

3. Egy mértani sorozat első tagja 10^23, és kvóciense 0,001.
a) Hányadik tagja a sorozatnak a 100?

b) Hány olyan tagja van a sorozatnak, amely nagyobb, mint 10^10?

NÉV:
Azonosító:
Eredmény: /