34. Statisztikai jellemzők

Forrás: https://www.tankonyvkatalogus.hu/storage/pdf/OH-MAT12TA__teljes.pdf

BEVEZETŐ

A szórást gyakran alkalmazzák a befektetések (pl. részvények) kockázatának mérésekor, mivel a változékonyabb árfolyamok, amelyek szórása nagyobb, több bizonytalanságot hordoznak.
(A múltbeli hozamok és szórások a jövőbeni árfolyamokat illetően azonban nem adnak egyértelmű információt.)
Ha egy részvény árfolyama az egyik évben 5%-kal emelkedik, akkor azt mondjuk rá, hogy a hozama 5%. Ha 5%-kal csökken, akkor a hozama -5%.
Ha egy részvény hozama három egymás utáni évben 6%, 4%, 5%, akkor az átlagos hozam ebben a három évben 5%.
Ha egy másik részvény hozama ugyanekkor 10%, -2% és 10%, akkor az átlagos hozam 6%, ami magasabb, mint az első részvény esetében, de jóval nagyobb a hozam szórása.
Ez a részvény kockázatosabb, mint az első.

KIDOLGOZOTT FELADAT

Táblázatba foglaltuk két részvény éves záró árfolyamát 5 egymást követo évben.
Kiszámoltuk, hogy a részvények árfolyama hány százalékkal nőtt vagy csökkent az előző évhez viszonyítva.
Ezt a százalékban megadott értéket nevezik (éves) hozamnak.
Határozd meg az egyes részvények esetében a hozamok szórását!
Ezen mutató alapján melyik részvény számít kockázatosabbnak?

Év 2018 2019 2020 2021 2022
A részvény árfolyama (Ft) 2600 2756 3060 3000 3150
A részvény hozama 6% 11% -2% 5%
B részvény árfolyama (Ft) 4700 5170 4963 5560 5670
B részvény hozama 10% -4% 12% 2%

Megoldás

Egy adatsokaság szórását megkapjuk, ha meghatározzuk az adatok átlagát, majd az adatoknak az átlagtól való eltérését.
Utána ezen eltéréseket négyzetre emeljük, majd meghatározzuk ezek átlagát, végül gyököt vonunk.
A számolásban segítségünkre lehet egy olyan táblázat, amely tartalmazza az adatokat (xi),
az adatoknak az átlagtól való eltérését (xi - x), valamint
az átlagtól való eltérés négyzetét ((xi - x)^2).
A hozamok átlaga az A részvény esetében x = 4 6 + 11 - 2 + 5 = 5, a B részvény esetében x = 4 10 - 4 +12 + 2 = 5.

A részvény 2019 2020 2021 2022
xi 6 11 -2 5
xi - x 1 6 -7 0
(xi - x)2 1 36 49 0

B részvény 2019 2020 2021 2020
xi 10 -4 12 2
xi - x 5 -9 7 -3
(xi - x)2 25 81 49 9

`sigma_A=sqrt((1+36+49+0)/4)=sqrt(21,5)≈4,64`
4 , , 1 36 49 0 21 5 4 64 A v = + + + = . , 4 25 81 49 9 41 6 40 B v = + + + = .
Az A részvény esetében az átlagos hozam 5%, és a hozam szórása 4,64%.
A B részvény esetében az átlagos hozam ugyancsak 5%, de a hozamok szórása nagyobb, 6,40%.
Ha két részvény esetén az átlagos hozam megegyezik, akkor azt tekintjük kockázatosabbnak, amelyiknek nagyobb a szórása.
Tehát ezen mutató alapján a B részvény a kockázatosabb, mivel éves hozama változékonyabb volt.
Megjegyzés:
Ha két részvény átlagos hozama különböző, akkor a relatív szórást szokták figyelembe venni, amit úgy kapunk meg, hogy a szórást elosztjuk az átlaggal.

ELMÉLET

szórás meghatározása (ismétlés)

(Jelölések: x: az adatok átlaga, v: az adatok szórása)
Számítsd ki az adatok átlagát!
x n x1 f xn = + + r
Vedd az adatok és az átlag különbségének négyzetét!
x x , , x x 1 n ^ - rh2 f ^ - rh2
Számold ki ezek átlagát (ez a szórásnégyzet)!
n x x x x 2 1 n 2 f 2 v = ^ - rh + +^ - rh
Vonj gyököt a szórásnégyzetből!
n x x

FELADAT

1. Táblázatba foglaltuk egy részvény éves záró árfolyamát forintban öt egymás utáni évben.

2015 2016 2017 2018 2019
6150 7380 7011 8063 8789

a) Határozd meg (a második évtol kezdve) a részvény hozamát, vagyis azt, hogy hány %-kal nőtt, illetve csökkent az árfolyam az elozo évhez viszonyítva!
✓ ✗
b) Határozd meg a hozamok átlagát és szórását!
✓ ✗

---

2. (Érettségi feladat nyomán, 2017)
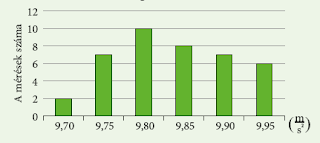
Egy fizikaórán a diákok a nehézségi gyorsulás, a g értékét határozták meg.
40 mérés eredményét tartalmazza a következő diagram.

Készíts gyakorisági táblázatot, majd határozd meg a 40 mérési eredmény móduszát, mediánját, átlagát és szórását!
✓ ✗

---

3. (Érettségi feladat, 2022)
Az ábrán látható diagram egy végzős évfolyam négy osztályában mutatja a fiúk és a lányok számát.

a) A legkisebb létszámú osztályban a lányok száma hány százaléka a fiúk számának?
✓ ✗
b) Töltsd ki a táblázatot, majd határozd meg a 4 adat terjedelmét, átlagát és szórását!
✓ ✗

Osztály 12. a 12. b 12. c 12. d
Lányok létszáma

c) A 12. b osztályban év végén a lányok matematikajegyeinek átlaga 4,5, az egész osztály matematikajegyeinek átlaga pedig 4,1 volt.
Mennyi volt év végén a 12. b osztályban a fiúk jegyeinek átlaga matematikából?
✓ ✗

HÁZI FELADAT

1. Egy részvény árfolyama négy egymás utáni évben 15; 12; 3, illetve 8%-kal nőtt.
Ezt úgy is megfogalmazhatjuk, hogy a részvény hozama ebben a négy évben 15%, 12%, 3% és 8% volt.
Határozd meg a hozamok átlagát és szórását!

---

2. A táblázat egy serdülő-röplabdacsapat játékosainak testmagasságát tartalmazza.

Adat (cm) 168 170 171 172 175
Gyakoriság 2 3 4 3 3

Határozd meg az adatok átlagát és szórását!

NÉV:
Azonosító:
Eredmény: /