Bevezető
A halmazelmélet számos tudományterület alapját képezi.Halmazokra épül a biológiában a rendszertan.
A fizika és a kémia is csoportosítja és halmazokba sorolja az anyagokat.
A matematikán belül a számhalmazokat az algebra, a ponthalmazokat a geometria vizsgálja.
A függvények esetében két halmaz elemei közötti hozzárendelésről beszélünk.
A kombinatorikában olyan feladatokkal találkozunk, ahol egy véges halmaz elemeit rendezzük sorba, vagy egy véges halmaz elemei közül választunk ki néhányat.
A gráfokat úgy határozzuk meg, mint pontok (más szóval csúcsok) és bizonyos pontokat összekötő élek halmaza.
A matematikában a halmaz és a halmaz eleme alapfogalmak.
Ez azt jelenti, hogy ezeket a fogalmakat nem vezetjük vissza egyszerűbb fogalmakra, azaz nem definiáljuk.
FOGALMAK, TÉTELEK, MÓDSZEREK
1. HALMAZOK
| Alapfogalmak |
halmaz, halmaz eleme Jelölés: A = {2; 3; 5; 7} esetén 2 ∈ A, 12 ∉ A |
|
| M | Halmaz megadása |
Akkor mondjuk, hogy megadtunk egy halmazt, ha minden dologról eldönthető, hogy
eleme-e a halmaznak, vagy sem. Egy halmaznak nincs két azonos eleme. Egy halmaz megadható például: – annak megfogalmazásával, hogy milyen tulajdonságú elemek tartoznak a halmazba; – az elemek felsorolásával; – jelekkel, ábrákkal; – halmazok és halmazműveletek segítségével. Például: A = {egyjegyű prímszámok} = {2; 3; 5; 7} = {n ∈ N|n prím és n < 10} A halmazokat szokás Venn-diagrammal szemléltetni. A számhalmazok hagyományos jelölését a Számtan, algebra témakörben találod. |
| D | Halmazok egyenlősége | Két halmaz pontosan akkor egyenlő, ha ugyanazok az elemeik. |
| D | Üres halmaz |
Ha a halmaznak nincs eleme, akkor üres halmaznak nevezzük. Jele: ∅ vagy { } |
| D | Véges halmaz | Ha egy halmaz elemeinek száma megadható egy természetes számmal, akkor véges halmaznak nevezzük. |
| D | Végtelen halmaz |
Olyan halmaz, amely nem véges. Vagyis bármilyen természetes számot adunk meg, a halmaznak több eleme van ennél. Végtelen halmaz például az egész számok halmaza, egy körvonal pontjainak halmaza, a koordináta-rendszer rácspontjainak halmaza. |
| D | Véges halmaz számossága | Véges halmaz számossága egyenlő az elemeinek a számával. Jele: |A| |
| D | Részhalmaz Valódi részhalmaz |
Egy A halmaz részhalmaza egy B halmaznak, ha az A halmaz minden eleme egyúttal eleme a B halmaznak is. Jele: A ⊆ B (Az A és a B halmaz lehet egyenlő.) Ha az A halmaz részhalmaza a B halmaznak, és B-nek van olyan eleme, amely nem eleme A-nak, akkor az A valódi részhalmaza B-nek. Jele: A ⊂ B. |
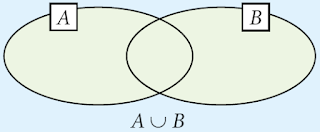
| D | Unió (egyesítés) | Az A és a B halmaz uniója azoknak az elemeknek a halmaza, amelyek legalább az egyik halmaznak elemei (azaz benne vannak az A vagy a B halmazban). Jele: A U B |
| D | Metszet (közös rész) | Az A és a B halmaz metszete azoknak az elemeknek a halmaza, amelyek mindkét halmaznak elemei (azaz benne vannak az A és a B halmazban is). Jele: A ⋂ B |
| D | Különbséghalmaz | Az A és a B halmaz különbséghalmaza azoknak az elemeknek a halmaza, amelyek elemei az A halmaznak, de nem elemei a B halmaznak. Jele: A \ B |
| D | Komplementer halmaz | Ha az A halmaz részhalmaza a H halmaznak, akkor a H \ A halmazt az A halmaz H-ra vonatkozó komplementer halmazának nevezzük. Jele: `bar(A)` |
| T | Szitaformula | Két véges halmaz uniójának elemszámát megkapjuk, ha a halmazok számosságának összegéből
kivonjuk a metszet számosságát. |A U B| = |A| + |B| - |A ⋂ B| Három véges halmaz esetén: |A U B U C| = |A| + |B| + |C| - |A ⋂ B| - |A ⋂ C| - |B ⋂ C| + |A ⋂ B ⋂ C| |
2. LOGIKA
| D | Állítás, kijelentés Állítás logikai értéke |
A logikában azokat a kijelentő mondatokat, amelyekről egyértelműen eldönthető, hogy a tartalmuk igaz vagy hamis, állításoknak vagy kijelentéseknek nevezzük. Egy állítás igaz vagy hamis, harmadik eset nincs. Az igaz, illetve a hamis megjelölés az állítás logikai értéke. |
|||||||||||||||
| D | Állítás tagadása (negáció) | Egy A állítás tagadása az az állítás, amely akkor és csak akkor igaz, ha az A állítás hamis. Jele: ¬A
|
|||||||||||||||
| D | VAGY művelet (diszjunkció) | Ha A és B egy-egy állítás, akkor A vagy B azt az állítást jelenti, amely igaz, ha A és B közül legalább az egyik igaz, és hamis, ha A és B is hamis. Ez a művelet a „megengedő vagy” művelet. Jele: A V B
|
|||||||||||||||
| D | ÉS művelet (konjunkció) | Ha A és B egy-egy állítás, akkor A és B azt az állítást jelenti, amely igaz, ha A is és B is igaz, és hamis, ha A és B közül legalább az egyik hamis. Jele: A ⋀ B
|
|||||||||||||||
| D | Kizáró vagy | Ha A és B egy-egy állítás, akkor a „vagy A, vagy B” azt az állítást jelenti, amely igaz, ha A és B közül pontosan az egyik igaz, minden más esetben hamis. Ez a művelet a „kizáró vagy” művelet. (Jele: A ⊕ B.)
|
|||||||||||||||
| D | „Ha …, akkor” művelet (implikáció) | Ha A és B egy-egy állítás, akkor a „ha A, akkor B” állítás pontosan akkor hamis, ha A igaz, és B hamis, minden más esetben igaz. Jele: A → B
|
|||||||||||||||
| D | „Akkor és csak akkor” művelet (ekvivalencia) | Ha A és B egy-egy állítás, akkor az „ A akkor és csak
akkor, ha B” azt az állítást jelenti, amely pontosan akkor igaz, ha A és B logikai értéke azonos, azaz vagy mindkettő igaz, vagy mindkettő hamis.
Minden más esetben hamis. Jele: A ↔ B
|
|||||||||||||||
| M | Állítás megfordítása | Egy „ha A, akkor B” (A → B) állítás megfordítása a „ha B, akkor A” (B → A) állítás. Az eredeti és a megfordított állítás igazságértéke független egymástól. Például: állítás: Ha egy négyszög téglalap, akkor átlói felezik egymást. megfordítása: Ha egy négyszög átlói felezik egymást, akkor téglalap. (Most az első állítás igaz, a második hamis.) |
3. KOMBINATORIKA
| D | Faktoriális | n! = 1 ∙ 2 ∙ … ∙ n (n ∈ Z+) Értelmezzük a 0!-t is: 0! = 1. |
| T | Sorba rendezés | n darab különböző elem lehetséges sorba rendezéseinek száma: n! (n ∈ Z+) (n darab elem egy lehetséges sorba rendezését az n elem egy permutációjának nevezzük.) Például: 5 különböző elem lehetséges sorba rendezéseinek száma 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 5! = 120 |
| T | Kiválasztás, ha számít a kiválasztott elemek sorrendje | n darab különböző elem közül kiválasztunk k darabot, és számít a kiválasztott elemek sorrendje.
(n, k ∈ Z+, n ≥ k) – Ha minden elemet legfeljebb egyszer választhatunk, akkor a lehetőségek száma: n ∙ (n - 1) ∙ … ∙ (n - k + 1) – Ha az elemek akár többször is kiválaszthatók, akkor a lehetőségek száma nk. (Ha n darab elem közül kiválasztunk k darabot, és számít a kiválasztott elemek sorrendje, akkor egy lehetséges kiválasztást az n elem egy k-ad osztályú variációjának nevezzük.) Például: 8 versenyző között az első három helyezett 8 ∙ 7 ∙ 6 = 336- féleképpen alakulhat ki, ha nincs holtverseny. Ha háromszor dobunk egy dobókockával, és a dobások eredményét sorban felírjuk, akkor a lehetőségek száma 6³ = 216. |
| D | Binomiális együttható | Az `((n),(k))` kifejezéseket binomiális együtthatóknak nevezzük. (n, k ∈ N, n ≥ k) `((n),(k))=(n!)/(k!*(n-k)!)` |
| T | Kiválasztás, ha nem számít a kiválasztott elemek sorrendje | n darab különböző elem közül kiválasztunk k darabot, nem számít a kiválasztott elemek sorrendje, és minden elemet legfeljebb egyszer választhatunk. (n, k ∈ N+, n ≥ k) A lehetőségek száma: `((n),(k))` (Ha n elem közül kiválasztunk k darabot, és nem számít a kiválasztott elemek sorrendje, akkor egy lehetséges kiválasztást az n elem egy k-ad osztályú kombinációjának nevezzük.) Például: 8 gyerek közül `((8),(3))=(8*7*6)/(3!)` = 56-féleképpen választhatunk ki egy 3 gyerekből álló csoportot, ha a csoport tagjainak sorrendje nem számít. |
| T | Összefüggések binomiális együtthatók között | `((n),(k)) = ((n),(n-k))` `((n),(n))=1` `((n),(0))=1` `((n),(n))=n` |
| T | k elemű részhalmazok száma | Egy n elemű halmaz k elemű részhalmazainak száma `((n),(k))`. (n, k ∈ N, n ≥ k) |
| T | Összes részhalmaz száma | Egy n elemű halmaz összes részhalmazainak száma 2n. (n ∈ N) |
4. GRÁFOK
| D | Gráf | Pontok (más szóval csúcsok) és bizonyos pontokat összekötő élek halmaza. |
| D | Fokszám | Egy csúcs fokszáma egyenlő az adott csúcsból kiinduló élek számával. |
| T | Fokszámok összege | Minden gráfban a pontok fokszámának összege egyenlő az élek számának kétszeresével. Ebből következik, hogy a fokszámok összege mindig páros. |
KIDOLGOZOTT FELADAT
1. Egy osztályban 17-en vannak, akik látták az Avatar, 18-an, akik látták a Mátrix, és 13-an, akik látták a Gladiátor című filmet.
Ugyanannyian vannak azok, akik mindhárom filmet látták, akik a három közül pontosan két filmet, akik pontosan egy filmet, és akik egy filmet sem láttak.
Hányan vannak az osztályban?
Ugyanannyian vannak azok, akik mindhárom filmet látták, akik a három közül pontosan két filmet, akik pontosan egy filmet, és akik egy filmet sem láttak.
Hányan vannak az osztályban?
2. Hány olyan 5 jegyű szám van, amelynek az utolsót kivéve mindegyik számjegye nagyobb, mint a rákövetkező?
3. Egy hivatalos megbeszélésen 6 cégvezető találkozott egymással.
Érkezéskor mindenki mindenkivel kezet fogott pontosan egyszer.
Minden kézfogást megörökített egy hivatalos fotós.
a) Hány kézfogás történt összesen?
b) A rendezvény honlapjára fotódokumentáció is felkerült a kézfogásokról.
Hányféleképpen választhatták ki a szerkesztők, hogy melyik képeket teszik a honlapra, ha az is lehet, hogy minden kézfogásról felteszik a képet, az is lehet, hogy kevesebbről?
(Legalább egy képet mindenképpen feltesznek, és a kiválasztás sorrendje nem számít.)
Érkezéskor mindenki mindenkivel kezet fogott pontosan egyszer.
Minden kézfogást megörökített egy hivatalos fotós.
a) Hány kézfogás történt összesen?
b) A rendezvény honlapjára fotódokumentáció is felkerült a kézfogásokról.
Hányféleképpen választhatták ki a szerkesztők, hogy melyik képeket teszik a honlapra, ha az is lehet, hogy minden kézfogásról felteszik a képet, az is lehet, hogy kevesebbről?
(Legalább egy képet mindenképpen feltesznek, és a kiválasztás sorrendje nem számít.)
FELADATOK I. RÉSZ
A1. Az A halmaz elemei a 120 pozitív osztói, a B halmaz elemei pedig a 150 pozitív osztói.
Elemei felsorolásával add meg az A ⋂ B és az A \ B halmazokat!
Elemei felsorolásával add meg az A ⋂ B és az A \ B halmazokat!
A2. A felsorolt halmazok közül melyek a végtelen halmazok?
N ⋂ R
N U R
N \ R
R \ N
N ⋂ R
N U R
N \ R
R \ N
A3. Az A és B halmazokról tudjuk, hogy |A| = 10 és |B| = 13.
a) Add meg A ⋂ B számosságának legnagyobb lehetséges értékét!
b) Add meg B \ A számosságának legkisebb lehetséges értékét!
a) Add meg A ⋂ B számosságának legnagyobb lehetséges értékét!
b) Add meg B \ A számosságának legkisebb lehetséges értékét!
A4. Rajzolj egy olyan gráfot, amelynek 5 csúcsa és 7 éle van, és minden csúcs fokszáma kisebb 4-nél!
A5. Hét ember érkezik egy terembe (közöttük Péter), és egyesével, egymás után lépnek be az ajtón.
Hányféle sorrendben léphetnek be, ha tudjuk, hogy közülük Péter nem másodikként lép a terembe?
Hányféle sorrendben léphetnek be, ha tudjuk, hogy közülük Péter nem másodikként lép a terembe?
A6. Hány olyan négyjegyű pozitív egész szám van, amelyben szerepel az ötös számjegy?
A7. Egy házban nyári szálláshelyként két különálló apartmant alakítottak ki.
Egyik héten az egyik apartmant a négytagú Sallai család, a másik apartmant az öttagú Kemény család vette ki.
A két család tagjai a héten megismerkedtek egymással, és összebarátkoztak, annak ellenére, hogy korábban senki nem ismert senkit a másik családból.
Ha senkit sem tekintünk önmaga ismerősének, akkor hány ismeretség van a 9 ember között
a) a nyaralás kezdetekor;
b) a nyaralás végén?
Egyik héten az egyik apartmant a négytagú Sallai család, a másik apartmant az öttagú Kemény család vette ki.
A két család tagjai a héten megismerkedtek egymással, és összebarátkoztak, annak ellenére, hogy korábban senki nem ismert senkit a másik családból.
Ha senkit sem tekintünk önmaga ismerősének, akkor hány ismeretség van a 9 ember között
a) a nyaralás kezdetekor;
b) a nyaralás végén?
A8. Hány részhalmaza van a 15-nél kisebb pozitív páros számok halmazának?
Indokold a válaszodat!
Indokold a válaszodat!
A9. Hány pontja és hány éle van annak a gráfnak, amelynek pontjai megfelelnek egy kocka oldallapjainak, és két pont között pontosan akkor fut él, ha a lapok szomszédosak?
A10. Anikó a következőt állítja:
Minden országban él kenguru.
Az alábbi négy állítás közül válaszd ki az összeset, amely Anikó állításának tagadása!
A: Semelyik országban sem élnek kenguruk.
B: Van olyan ország, amelyben nem él kenguru.
C: Van olyan ország, amelyben él kenguru.
D: Nem minden országban él kenguru.
Minden országban él kenguru.
Az alábbi négy állítás közül válaszd ki az összeset, amely Anikó állításának tagadása!
A: Semelyik országban sem élnek kenguruk.
B: Van olyan ország, amelyben nem él kenguru.
C: Van olyan ország, amelyben él kenguru.
D: Nem minden országban él kenguru.
A11. Határozd meg az A, a B, az A⋀ ¬B és az A V ¬B állítások logikai értékét!
A: Van olyan halmaz, amelynek a számossága 0.
B: Van olyan gráf, amelynek ugyanannyi éle van, mint pontja.
Válaszodat indokold!
A: Van olyan halmaz, amelynek a számossága 0.
B: Van olyan gráf, amelynek ugyanannyi éle van, mint pontja.
Válaszodat indokold!
A12. Egy kerékpáros lámpában 5 LED (LED = fényt kibocsátó dióda) van.
A LED-ek egymástól függetlenül működhetnek, legalább egy LED mindig világít, ha a lámpa be van kapcsolva.
a) Hány különböző módon világíthat a lámpa, ha két világítást akkor tekintünk különbözőnek, ha nem ugyanazok a LED-ek világítanak?
b) Hány lehetőség van akkor, ha mindegyik LED fehéren vagy pirosan világíthat?
A LED-ek egymástól függetlenül működhetnek, legalább egy LED mindig világít, ha a lámpa be van kapcsolva.
a) Hány különböző módon világíthat a lámpa, ha két világítást akkor tekintünk különbözőnek, ha nem ugyanazok a LED-ek világítanak?
b) Hány lehetőség van akkor, ha mindegyik LED fehéren vagy pirosan világíthat?
FELADATOK I. RÉSZ
B1. Az A és a B halmazokról tudjuk, hogy A U B = {egyjegyű pozitív egész számok}, A ⋂ B = {6 pozitív osztói} és A \ B = {4; 5}.
Elemei felsorolásával add meg az A és a B halmazokat!
Elemei felsorolásával add meg az A és a B halmazokat!
B2. Legyen az A halmaz a [2; 6] zárt intervallum, a B halmaz pedig a [3; 10] zárt intervallum.
Határozd meg az A U B és az A ⋂ B halmazokat!
Határozd meg az A U B és az A ⋂ B halmazokat!
B3. Az ábrán látható gráfot hány éllel kell kiegészíteni ahhoz, hogy
a) bármely két csúcsa között pontosan egy él fusson;
b) minden csúcsának a fokszáma 5 legyen?
a) bármely két csúcsa között pontosan egy él fusson;
b) minden csúcsának a fokszáma 5 legyen?
B4. Határozd meg az A, a B és az A ⋀ ¬B állítások logikai értékét!
Indokold a válaszodat!
A: Minden deltoid tengelyesen szimmetrikus.
B: Minden paralelogramma tengelyesen szimmetrikus.
Indokold a válaszodat!
A: Minden deltoid tengelyesen szimmetrikus.
B: Minden paralelogramma tengelyesen szimmetrikus.
B5. Egy héttagú csoportban minden tagnak pontosan két ismerőse van a csoport tagjai között.
Szemléltess gráffal egy ilyen ismeretségi rendszert!
(Az ismeretség kölcsönös, és senki sem ismerőse saját magának.)
Szemléltess gráffal egy ilyen ismeretségi rendszert!
(Az ismeretség kölcsönös, és senki sem ismerőse saját magának.)
B6. Egy 8 főből álló baráti társaság moziba megy.
Arnold a társaság egyik tagja. Hányféleképpen ülhetnek le egy 8 ülésből álló sorba úgy, hogy Arnold üljön a sor valamelyik szélén?
Arnold a társaság egyik tagja. Hányféleképpen ülhetnek le egy 8 ülésből álló sorba úgy, hogy Arnold üljön a sor valamelyik szélén?
B7. Legyenek a és b valós számok. Adott a következő állítás:
„Ha a abszolút értéke és b abszolút értéke egyenlő, akkor a és b egyenlő.”
a) Határozd meg az állítás logikai értékét!
b) Fogalmazd meg az állítás megfordítását!
c) Határozd meg a b)-ben kimondott állítás logikai értékét!
„Ha a abszolút értéke és b abszolút értéke egyenlő, akkor a és b egyenlő.”
a) Határozd meg az állítás logikai értékét!
b) Fogalmazd meg az állítás megfordítását!
c) Határozd meg a b)-ben kimondott állítás logikai értékét!
B8. Mely halmazok végtelenek az alábbiak között?
R + Z
Z + N
R + ∅
R \ ∅
∅ \ R
R + Z
Z + N
R + ∅
R \ ∅
∅ \ R
B9. Egy 10 elemű halmaznak hány olyan részhalmaza van, amelynek legalább 7 eleme van?
B10. Egy kötélen néhány zokni szárad.
Tekintsük a következő állítást:
A kötélen minden zokni fekete.
Válaszd ki az alábbiak közül az összes állítást, amely tagadása a fentinek!
A: A kötélen minden zokni fehér.
B: A kötélen nincs fekete zokni.
C: Van olyan zokni a kötélen, amely nem fekete.
D: A kötélen nem minden zokni fekete.
Tekintsük a következő állítást:
A kötélen minden zokni fekete.
Válaszd ki az alábbiak közül az összes állítást, amely tagadása a fentinek!
A: A kötélen minden zokni fehér.
B: A kötélen nincs fekete zokni.
C: Van olyan zokni a kötélen, amely nem fekete.
D: A kötélen nem minden zokni fekete.
B11. Egy 34 fős osztály 2 képviselőt választ a diákönkormányzatba és 4 felelőst az iskolai közösségi szolgálatot szervező csoportba.
A 2 képviselő sorrendje és a 4 felelős sorrendje nem számít.
Hányféle lehet a választás eredménye, ha senkit sem választanak meg két tisztségre?
A 2 képviselő sorrendje és a 4 felelős sorrendje nem számít.
Hányféle lehet a választás eredménye, ha senkit sem választanak meg két tisztségre?
B12. Hány olyan ötjegyű szám van, amelynek
a) mindegyik számjegye páros;
b) mindegyik számjegye különböző?
a) mindegyik számjegye páros;
b) mindegyik számjegye különböző?
FELADATOK II. RÉSZ
P1. Egy gyógytornász minden hétfőn, szerdán és pénteken tart úszásfoglalkozást gyerekeknek.
Nincs olyan tanítványa, aki mindhárom nap jár úszni.
Hétfőn és szerdán 14-en járnak, szerdán és pénteken 18-an, hétfőn és pénteken 8-an. Összesen 65 gyerek jár hozzá úszni, és ugyanannyian járnak hétfőn, szerdán és pénteken is.
a) Hányan vannak, akik csak pénteken járnak hozzá úszni?
b) A gyógytornászt felkérték, hogy tartson egy rövid bemutatófoglalkozást.
Hányféleképpen választhat ki az úszásra járó tanítványai közül egy 5 gyerekből álló csoportot, akikkel a bemutatófoglalkozást tartja?
c) Az egyik alkalommal az úszáson részt vevők közül 5 gyerek (köztük Anna és Péter) megkérte, hogy hadd versenyezzenek.
Hányféle végeredmény születhetett a versenyen, ha tudjuk, hogy Anna előrébb végzett, mint Péter, és a versenyen nem volt holtverseny?
Nincs olyan tanítványa, aki mindhárom nap jár úszni.
Hétfőn és szerdán 14-en járnak, szerdán és pénteken 18-an, hétfőn és pénteken 8-an. Összesen 65 gyerek jár hozzá úszni, és ugyanannyian járnak hétfőn, szerdán és pénteken is.
a) Hányan vannak, akik csak pénteken járnak hozzá úszni?
b) A gyógytornászt felkérték, hogy tartson egy rövid bemutatófoglalkozást.
Hányféleképpen választhat ki az úszásra járó tanítványai közül egy 5 gyerekből álló csoportot, akikkel a bemutatófoglalkozást tartja?
c) Az egyik alkalommal az úszáson részt vevők közül 5 gyerek (köztük Anna és Péter) megkérte, hogy hadd versenyezzenek.
Hányféle végeredmény születhetett a versenyen, ha tudjuk, hogy Anna előrébb végzett, mint Péter, és a versenyen nem volt holtverseny?
P2. Egy pozitív egész szám pozitív osztói ábrázolhatók gráf segítségével úgy, hogy a gráf csúcsai az osztók, és két csúcs között akkor fut él, ha az egyik csúcsban lévő szám osztója vagy többszöröse a másik csúcsban lévő számnak.
a) Helyezd el a 63 pozitív osztóit az ábra szerinti gráf csúcsaiban a leírt szabálynak megfelelően!
b) Hányféle szabályos kitöltése van az ábra szerinti gráfnak a 63 pozitív osztóival a leírt szabálynak megfelelően?
Válaszodat indokold!
c) Hányféleképpen választhatunk ki a 63 pozitív osztói közül valahány osztót, ha legalább egyet kiválasztunk, és a kiválasztás sorrendje nem számít?
a) Helyezd el a 63 pozitív osztóit az ábra szerinti gráf csúcsaiban a leírt szabálynak megfelelően!
b) Hányféle szabályos kitöltése van az ábra szerinti gráfnak a 63 pozitív osztóival a leírt szabálynak megfelelően?
Válaszodat indokold!
c) Hányféleképpen választhatunk ki a 63 pozitív osztói közül valahány osztót, ha legalább egyet kiválasztunk, és a kiválasztás sorrendje nem számít?
P3. Egy édesipari cég olyan dobozba csomagolja az egyik termékét, amelynek az alakja négyoldalú szabályos csonkagúla.
a) A cég úgy dönt, hogy a doboz fedőlapját és az oldallapokat kék, zöld, lila vagy sárga színűre színezik olyan módon, hogy a szomszédos oldallapok különböző színűek.
Hány különböző doboz készíthető e négy szín használatával?
(Minden lap egyszínű, az alaplap fehér, a doboz mérete adott, és két dobozt különbözőnek tekintünk, ha forgatással nem vihetők egymásba.)
b) Döntsd el az alábbi állításról, hogy igaz vagy hamis!
Indokold a válaszodat!
Ha egy test csonkagúla, akkor van két olyan lapja, amelyek területe különböző.
c) Fogalmazd meg a b)-ben megadott állítás megfordítását, és add meg a logikai értékét!
Indokold a válaszodat!
a) A cég úgy dönt, hogy a doboz fedőlapját és az oldallapokat kék, zöld, lila vagy sárga színűre színezik olyan módon, hogy a szomszédos oldallapok különböző színűek.
Hány különböző doboz készíthető e négy szín használatával?
(Minden lap egyszínű, az alaplap fehér, a doboz mérete adott, és két dobozt különbözőnek tekintünk, ha forgatással nem vihetők egymásba.)
b) Döntsd el az alábbi állításról, hogy igaz vagy hamis!
Indokold a válaszodat!
Ha egy test csonkagúla, akkor van két olyan lapja, amelyek területe különböző.
c) Fogalmazd meg a b)-ben megadott állítás megfordítását, és add meg a logikai értékét!
Indokold a válaszodat!
P4. Egy dobókockát egymás után háromszor feldobunk.
Ha a dobások sorrendjét is figyelembe vesszük, akkor hányféleképpen fordulhat elő, hogy
a) mindegyik esetben ugyanazt a számot dobjuk;
b) három különböző számot dobunk;
c) a három szám között pontosan kettő ugyanaz;
d) a dobott pontok összege 16?
Ha a dobások sorrendjét is figyelembe vesszük, akkor hányféleképpen fordulhat elő, hogy
a) mindegyik esetben ugyanazt a számot dobjuk;
b) három különböző számot dobunk;
c) a három szám között pontosan kettő ugyanaz;
d) a dobott pontok összege 16?
P5. Egy zsákban 30 darab számozott golyó van.
Az 1-től 10-ig számozott golyók színe fehér, a 11-től 20-ig számozottak színe fekete, és a 21-től 30-ig számozottak színe zöld.
A golyók tapintásra egyformák.
Becsukott szemmel, visszatevés nélkül kihúzunk a zsákból néhány golyót.
A kihúzott golyók sorrendje nem számít. (Két húzás azonos, ha ugyanazokat a golyókat húztuk ki.)
a) Hány golyót kell kihúzni a zsákból, hogy biztosan legyen a kihúzott golyók között fekete vagy fehér?
b) Hány golyót kell kihúzni a zsákból, hogy biztosan legyen a kihúzott golyók között fekete és fehér?
c) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben mindegyik golyó fehér?
d) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben a golyók közül legalább kettő fehér?
e) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben a golyók közül pontosan kettő fehér, és pontosan kettőn 10-zel osztható szám áll?
Az 1-től 10-ig számozott golyók színe fehér, a 11-től 20-ig számozottak színe fekete, és a 21-től 30-ig számozottak színe zöld.
A golyók tapintásra egyformák.
Becsukott szemmel, visszatevés nélkül kihúzunk a zsákból néhány golyót.
A kihúzott golyók sorrendje nem számít. (Két húzás azonos, ha ugyanazokat a golyókat húztuk ki.)
a) Hány golyót kell kihúzni a zsákból, hogy biztosan legyen a kihúzott golyók között fekete vagy fehér?
b) Hány golyót kell kihúzni a zsákból, hogy biztosan legyen a kihúzott golyók között fekete és fehér?
c) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben mindegyik golyó fehér?
d) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben a golyók közül legalább kettő fehér?
e) Öt golyót húzunk ki.
Hány olyan húzás van, amelyben a golyók közül pontosan kettő fehér, és pontosan kettőn 10-zel osztható szám áll?
FELADATOK II. RÉSZ
Q1. a) Az A halmazban a kételemű részhalmazok száma 1575-tel több, mint az egyelemű részhalmazok számának 50-szerese.
Hány elemű az A halmaz?
b) A B halmaz elemei azok a 100-nál kisebb pozitív egész számok, amelyek nem oszthatók sem 2-vel, sem 7-tel, sem 11-gyel.
Hány elemű a B halmaz?
Hány elemű az A halmaz?
b) A B halmaz elemei azok a 100-nál kisebb pozitív egész számok, amelyek nem oszthatók sem 2-vel, sem 7-tel, sem 11-gyel.
Hány elemű a B halmaz?
Q2. Egy sakkversenyt körmérkőzéses rendszerben bonyolítanak le, azaz mindenki mindenkivel pontosan egy partit játszik.
Táblázatba foglaltuk, hogy eddig ki kivel játszott, a partit ki nyerte, vagy a parti döntetlenre végződött.
(Például a táblázatba dőlt betűvel írt Anna azt jelenti, hogy Anna és Béla már játszott egymással, és azt a partit Anna nyerte.)
a) Szemléltesd gráffal a versenyen lejátszott partikat úgy, hogy a gráf pontjai jelentsék a versenyzőket, a gráf élei pedig az eddig lejátszott partikat!
b) A versenyen hetente egy fordulót rendeznek meg.
Egy fordulóban mindenki pontosan egy partit játszik.
Hány forduló van még hátra a versenyből?
c) A győzelemért 1 pont, a döntetlenért 0,5 pont, a vesztes partiért 0 pont jár.
Kinek hány pontja van a verseny jelenlegi állásában?
Táblázatba foglaltuk, hogy eddig ki kivel játszott, a partit ki nyerte, vagy a parti döntetlenre végződött.
(Például a táblázatba dőlt betűvel írt Anna azt jelenti, hogy Anna és Béla már játszott egymással, és azt a partit Anna nyerte.)
| Anna | Béla | Cili | Dani | Ede | Feri | |
| Anna | - | Anna | Ede | Feri | ||
| Béla | - | - | Béla | döntetlen | ||
| Cili | - | - | - | Dani | Cili | |
| Dani | - | - | - | - | döntetlen | |
| Ede | - | - | - | - | - | Feri |
| Feri | - | - | - | - | - | - |
b) A versenyen hetente egy fordulót rendeznek meg.
Egy fordulóban mindenki pontosan egy partit játszik.
Hány forduló van még hátra a versenyből?
c) A győzelemért 1 pont, a döntetlenért 0,5 pont, a vesztes partiért 0 pont jár.
Kinek hány pontja van a verseny jelenlegi állásában?
| Név | Anna | Béla | Cili | Dani | Ede | Feri |
| Pontszám |
Q3. Hány olyan hatjegyű szám van,
a) amelyben szerepel a nyolcas számjegy;
b) amely háromféle számjegyet tartalmaz, mindegyik számjegyből kettőt;
c) amelyben a számjegyek különbözők, és növekvő sorrendben követik egymást?
a) amelyben szerepel a nyolcas számjegy;
b) amely háromféle számjegyet tartalmaz, mindegyik számjegyből kettőt;
c) amelyben a számjegyek különbözők, és növekvő sorrendben követik egymást?
Q4. Egy 30 fős érettségiző osztályban 18 tanulónak van középfokú nyelvvizsgája angol nyelvből vagy német nyelvből, közülük 3 tanulónak mindkét nyelvből.
Az angol nyelvvizsgával rendelkezők száma kétszerese a német nyelvvizsgával rendelkező tanulók számának.
Más nyelvből nem tett senki nyelvvizsgát az osztályban.
a) Hány tanulónak van német nyelvből középfokú nyelvvizsgája?
b) Hányféleképpen választható ki az osztály tanulói közül négy úgy, hogy legalább kettőnek legyen nyelvvizsgája, ha a kiválasztás sorrendje nem számít?
c) Hányféle sorrendben hívhatják be a szóbeli érettségi vizsgára a diákokat, ha először azokat hívják, akiknek két nyelvvizsgájuk van, utána azokat, akiknek egy, végül azokat, akiknek nincs nyelvvizsgájuk?
Az angol nyelvvizsgával rendelkezők száma kétszerese a német nyelvvizsgával rendelkező tanulók számának.
Más nyelvből nem tett senki nyelvvizsgát az osztályban.
a) Hány tanulónak van német nyelvből középfokú nyelvvizsgája?
b) Hányféleképpen választható ki az osztály tanulói közül négy úgy, hogy legalább kettőnek legyen nyelvvizsgája, ha a kiválasztás sorrendje nem számít?
c) Hányféle sorrendben hívhatják be a szóbeli érettségi vizsgára a diákokat, ha először azokat hívják, akiknek két nyelvvizsgájuk van, utána azokat, akiknek egy, végül azokat, akiknek nincs nyelvvizsgájuk?
Q5. Egy cégcsoport égisze alatt 7 vállalkozás működik.
A szervezet olyan forrásokra pályázhatott, amelyeket együttműködés keretében használhatnak fel.
Úgy döntöttek, hogy mindegyik pályázatukban pontosan 2 vállalkozás dolgozik együtt.
a) Az egyik megbeszélésen mind a 7 vállalkozásból egy-egy ember vesz részt.
A találkozó elején mindenki koccint a többi emberrel, mindenkivel pontosan egyszer.
Hány koccintás történik?
b) Bizonyítsd be, hogy nem lehetséges, hogy mind a 7 vállalkozás pontosan 3 projektben vesz részt!
c) Az év végén a forrást biztosító szervezet ellenőriz néhány befejezett projektet.
Hányféleképpen választhat ki 4 projektet a szervezet projektjei közül, ha a vállalkozások közül 4 vállalkozás 3 projektben, 3 vállalkozás pedig 2 projektben vett részt?
A szervezet olyan forrásokra pályázhatott, amelyeket együttműködés keretében használhatnak fel.
Úgy döntöttek, hogy mindegyik pályázatukban pontosan 2 vállalkozás dolgozik együtt.
a) Az egyik megbeszélésen mind a 7 vállalkozásból egy-egy ember vesz részt.
A találkozó elején mindenki koccint a többi emberrel, mindenkivel pontosan egyszer.
Hány koccintás történik?
b) Bizonyítsd be, hogy nem lehetséges, hogy mind a 7 vállalkozás pontosan 3 projektben vesz részt!
c) Az év végén a forrást biztosító szervezet ellenőriz néhány befejezett projektet.
Hányféleképpen választhat ki 4 projektet a szervezet projektjei közül, ha a vállalkozások közül 4 vállalkozás 3 projektben, 3 vállalkozás pedig 2 projektben vett részt?