BEVEZETŐ
Szotyi kutyusnak védőgallért kell viselnie néhány napig, hogy ne rághassa le a kötést, amelyet az állatorvos tett a lábára.A védőgallér alakja olyan, mint egy lámpaernyő, egy csonkakúp palástja.
ELMÉLET
A csonkagúla és a forgáskúpból származtatott csonkakúp felszíne az alaplap, a fedőlap és a palást területének összege:A = Talaplap + tfedőlap + Tpalást
A csonkakúp hálója két körlapból és a kiterített palástból áll.
A palást egy körgyűrűcikk.
Legyen a csonkakúp alapkörének sugara R, a fedőkörének sugara r, és az alkotója a hoszszúságú.
Bebizonyítható, hogy egy körgyűrűcikk területét megadja a határoló körívek hossza számtani közepének és a körgyűrű szélességének a szorzata:
T R r a 22 2
palást = r + r $ , ami egyszerűsítés után:
T R r a palást = ] + gr $
Így az egyenes csonkakúp felszíne:
A R2 r2 R r a R2 r2 R r a
Megjegyzés:
1. A palást területének kiszámítási módja nagyon hasonlít a trapéz területképletéhez (a két alap hosszának számtani közepét megszorozzuk a trapéz magasságával).2. A szabályos n oldalú csonkagúla hálója két n oldalú szabályos sokszögből és a kiterített palástból áll.
A palástot n darab egymással egybevágó szimmetrikus trapéz alkotja.
A felszín: A = T + t + n Ttrapéz
Ha a csonkagúla szabályos 4 oldalú, az alaplap éle a, a fedőlap éle b hosszúságú, és az oldallap magassága m, akkor az egyenes csonkagúla felszíne:
A a b 4 a 2 b m2 2
szabályos négyoldalú cs.g. = + + $ + $ ,
egyszerűbben: A a2 b2 2 a b m
szabályos négyoldalú cs.g. = + + ] + g $ .
A R2 r2 R r a
A a2 b2 2 a b m
FELADAT
1. (Javasoljuk páros munkában végezni.)
Két barát, Antal és Bandi terveket készít Szotyi kutyus védőgallérjának elkészítéséhez.
Először megmérik, hogy milyen hosszú a kutyus nyaka körül a pánt, amihez a gallért rögzítik.
Ezt 47 cm-nek találják, ami azt jelenti, hogy a csonkakúp fedőkörének sugara 2 , 47 . 7 5 r cm.
Úgy gondolják, ahhoz, hogy a fejét tudja valamennyire mozgatni, az alapkör átmérőjének 35 cm-nek kell lennie, és kb. 20 cm széles gallér elég ahhoz, hogy a kötéséhez ne férjen hozzá.
Ezek után Antal terve a következő: az egyszerűség kedvéért felvázol egy 35 cm-es oldalhosszú szabályos háromszöget.
Ha ezt megforgatja az egyik szimmetriatengelye körül, egy forgáskúpot kap.
Ebből levág egy 7,5 cm alapkör sugarú kis kúpot, és a megmaradt egyenes csonkakúp palástjából lesz Szotyi gallérja.
Vajon mekkora a gallér területe?
a) Indokold, hogy az ábrán szereplő adatok (15 cm és 20 cm) helyesek!
b) Mi a hasonlóság aránya a levágott kis kúp és a teljes kúp között?
Ezek után Antal felvázolja a teljes kúp palástját, és szétvágja két részre:
a kis kúp és a csonkakúp palástjára.
c) Készítsd el te is a palást vázlatát, és számítsd ki, hányad része a kis kúp palástja a teljes palástnak!
d) Hányad része a csonkakúp palástja a teljes palástnak?
Ezután Antal kiszámítja a teljes kúp palástjának a területét, amiből könnyen megkapja a csonkakúp palástjának a területét.
e) Mekkora Szotyi gallérjának a területe?
Készítsd el te is Antal vázlatrajzait, és végezd el a számításait!
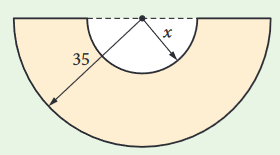
Bandi terve a következő: felvázol egy 35 cm sugarú félkört.
a) Mekkora lesz ennek a félkörívnek a hossza?
b) Mekkora sugarú, vele koncentrikus félkört vágjon ki belőle, hogy annak az ívhossza megegyezzen a csonkakúp fedőkörének kerületével?
A megmaradt körgyűrűcikkből csonkakúpot formál.
c) Mekkora a keletkezett csonkakúp alapkörének és fedőkörének a sugara, mekkorák az alkotók?
d) Mekkora a nagyobbik félkör, és mekkora a kisebbik félkör területe?
e) Mekkora Szotyi gallérjának (vagyis a csonkakúp palástjának) a területe?
Készíts vázlatrajzokat Bandi elgondolásához, és végezd el a számításait!
Hasonlítsd össze a két fiú számításainak eredményeit!
Két barát, Antal és Bandi terveket készít Szotyi kutyus védőgallérjának elkészítéséhez.
Először megmérik, hogy milyen hosszú a kutyus nyaka körül a pánt, amihez a gallért rögzítik.
Ezt 47 cm-nek találják, ami azt jelenti, hogy a csonkakúp fedőkörének sugara 2 , 47 . 7 5 r cm.
Úgy gondolják, ahhoz, hogy a fejét tudja valamennyire mozgatni, az alapkör átmérőjének 35 cm-nek kell lennie, és kb. 20 cm széles gallér elég ahhoz, hogy a kötéséhez ne férjen hozzá.
Ezek után Antal terve a következő: az egyszerűség kedvéért felvázol egy 35 cm-es oldalhosszú szabályos háromszöget.
Ha ezt megforgatja az egyik szimmetriatengelye körül, egy forgáskúpot kap.
Ebből levág egy 7,5 cm alapkör sugarú kis kúpot, és a megmaradt egyenes csonkakúp palástjából lesz Szotyi gallérja.
Vajon mekkora a gallér területe?
a) Indokold, hogy az ábrán szereplő adatok (15 cm és 20 cm) helyesek!
b) Mi a hasonlóság aránya a levágott kis kúp és a teljes kúp között?
Ezek után Antal felvázolja a teljes kúp palástját, és szétvágja két részre:
a kis kúp és a csonkakúp palástjára.
c) Készítsd el te is a palást vázlatát, és számítsd ki, hányad része a kis kúp palástja a teljes palástnak!
d) Hányad része a csonkakúp palástja a teljes palástnak?
Ezután Antal kiszámítja a teljes kúp palástjának a területét, amiből könnyen megkapja a csonkakúp palástjának a területét.
e) Mekkora Szotyi gallérjának a területe?
Készítsd el te is Antal vázlatrajzait, és végezd el a számításait!
Bandi terve a következő: felvázol egy 35 cm sugarú félkört.
a) Mekkora lesz ennek a félkörívnek a hossza?
b) Mekkora sugarú, vele koncentrikus félkört vágjon ki belőle, hogy annak az ívhossza megegyezzen a csonkakúp fedőkörének kerületével?
A megmaradt körgyűrűcikkből csonkakúpot formál.
c) Mekkora a keletkezett csonkakúp alapkörének és fedőkörének a sugara, mekkorák az alkotók?
d) Mekkora a nagyobbik félkör, és mekkora a kisebbik félkör területe?
e) Mekkora Szotyi gallérjának (vagyis a csonkakúp palástjának) a területe?
Készíts vázlatrajzokat Bandi elgondolásához, és végezd el a számításait!
Hasonlítsd össze a két fiú számításainak eredményeit!
2. Egy szabályos négyoldalú csonkagúla felszíne 274 cm2.
Az alapél hossza 11 cm, a fedőél hossza 5 cm.
Mekkora a csonkagúla oldallapjai magasságának és oldalélének hossza?
Mekkora szöget zár be az oldallap az alaplappal?
Az alapél hossza 11 cm, a fedőél hossza 5 cm.
Mekkora a csonkagúla oldallapjai magasságának és oldalélének hossza?
Mekkora szöget zár be az oldallap az alaplappal?
HÁZI FELADAT
1. A következő táblázat három egyenes csonkakúp néhány adatát tartalmazza.
R az alapkör sugarának, r a fedőkör sugarának, a az alkotóknak a hosszát jelöli cm-ben.
Az alapkör területe T, a fedőkör területe t, a palást területe P, a csonkakúp felszíne A cm2-ben.
a) Töltsd ki a táblázat üres celláit!
b) Határozd meg a táblázatban megadott csonkakúpok magasságát!
R az alapkör sugarának, r a fedőkör sugarának, a az alkotóknak a hosszát jelöli cm-ben.
Az alapkör területe T, a fedőkör területe t, a palást területe P, a csonkakúp felszíne A cm2-ben.
| R | r | a | T | t | P | A | |
| I. | 12 | 6 | 10 | ||||
| II. | 12 | 3 | 10 | ||||
| III. | 6,15 | 4,76 | 3,11 |
b) Határozd meg a táblázatban megadott csonkakúpok magasságát!
2. Egy szabályos négyoldalú csonkagúla felszíne 914 cm2.
Az alapél hossza 17 cm, az oldallapjai magasságának hossza 12 cm.
Határozd meg a fedőél hosszát, az oldalél és az alaplap hajlásszögét!
Az alapél hossza 17 cm, az oldallapjai magasságának hossza 12 cm.
Határozd meg a fedőél hosszát, az oldalél és az alaplap hajlásszögét!
NÉV:
Azonosító:
Eredmény: /