48. Függvények

Forrás: https://www.tankonyvkatalogus.hu/storage/pdf/OH-MAT12TA__teljes.pdf

Bevezető

A felismerés, hogy a körülöttünk lévő világ jelenségei egymással összefüggnek, egyidős az emberiséggel.
A matematikában azonban a függvény fogalma (legalábbis mai formájában) viszonylag későn alakult ki: a kifejezés Gottfried Leibniz német matematikus egy 1673-ban írt levelében bukkant fel először.
Az azóta eltelt három és fél évszázad alatt a függvények vizsgálata a matematika egyik leglátványosabb és leghasznosabb területévé nőtte ki magát.
Függvényekkel dolgozik a Mars-járót célba juttató mérnök, a tőzsdei elemző, a vírusok fertőzési gyorsaságát vizsgáló virológus.
A hétköznapi, gyakorlati életben is fontosak a függvénytani alapismeretek, hiszen azok nélkül nehezen lehetne megérteni például a heti időjárás-előrejelzést, vagy gondot okozna a hivatásos sofőrök vezetéssel kapcsolatos információkat tartalmazó tachográf (menetíró-készülék) elemzésének elvégzése.

FÜGGVÉNYEK

D	Függvény Értelmezési tartomány Értékkészlet	Legyen A és B két – egymástól nem feltétlenül különböző – nemüres halmaz. Függvénynek nevezzük azt a hozzárendelést, amely az A halmaz minden eleméhez a B halmazból pontosan egy elemet rendel. Ekkor a függvény értelmezési tartománya az A halmaz, képhalmaza a B halmaz. Értékkészlet: a B halmaz azon elemeinek halmaza, melyeket hozzárendelünk valamely értelmezési tartománybeli elemhez. Megjegyzés: A függvény tehát egyértelmű hozzárendelés. Az A és B halmazok nem csak számhalmazok lehetnek. Például: A Föld országaihoz hozzárendeljük a hivatalos fővárosukat. A = {a világ országai} B = {a világ városai}
D	Hozzárendelési szabály	A hozzárendelési szabály az az utasítás, amely egyértelműen megadja, hogy az értelmezési tartomány egyes elemeihez a képhalmaz melyik elemét kell hozzárendelni. A függvényeket általában az értelmezési tartománnyal és a hozzárendelési szabállyal szokás megadni. (Ha a számhalmazokon értelmezett függvényekre az értelmezési tartományt nem adják meg, akkor a valós számoknak azt a legbővebb részhalmazát tekintjük értelmezési tartománynak, amin a hozzárendelésnek értelme van.) Például: f : Rendeljük hozzá minden pozitív egész számhoz a háromszorosát. Ekkor a hozzárendelés szabálya a háromszorozás; az értelmezési tartomány a pozitív egész számok halmaza; az értékkészlet a hárommal osztható pozitív egész számok halmaza. g: Rendeljük hozzá minden valós számhoz az abszolút értékét. Ekkor a hozzárendelés szabálya az abszolútérték-képzés; az értelmezési tartomány a valós számok halmaza; az értékkészlet a nemnegatív valós számok halmaza.
D	Függvénytani jelölések	A függvények jele általában f , g, h … Értelmezési tartománya: Df , Dg, Dh … Értékkészlete: Rf , Rg, Rh … A hozzárendelést a ↦ szimbólum jelöli. Az értelmezési tartomány és a képhalmaz közé → szimbólum kerül. Például: Az előbbi példák jelölésekkel: f : N → R; x ↦ 3x; Df = N; Rf = {0; 3; 6; 9; …} = {3x|x ∈ N} g : R → R; x ↦ |x|; Dg = R; Rg = R0+ Leírhatók a hozzárendelések f : N → R; f (x) = 3x; g : R → R; g(x) = |x| módon is.
D	Helyettesítési érték	Ha x0 az f függvény értelmezési tartományának eleme, akkor a függvény x0 helyen felvett helyettesítési értéke (röviden: függvényértéke): a képhalmaznak az az eleme, amit a függvény x0-hoz rendel. Jele: f (x0) Például: Az f (x) = 3x függvénynek az 5 helyen felvett helyettesítési értéke f (5) = 3 ∙ 5 = 15; a g (x) = |x| függvény értéke a -7,2 helyen g(-7,2) = |-7,2| = 7,2.
D	Kölcsönösen egyértelmű függvény	Ha egy függvény az értelmezési tartomány bármely két különböző eleméhez az értékkészlet különböző elemeit rendeli, akkor a függvény kölcsönösen egyértelmű. Például: Az f : N → R; f (x) = 3x függvény kölcsönösen egyértelmű; a g : R → R; g (x) = |x| függvény nem kölcsönösen egyértelmű, mert például a -3-hoz és a 3-hoz ugyanazt az értéket, a 3-at rendeli.
D	Függvény megfordítása	Legyen f az A halmazon értelmezett kölcsönösen egyértelmű függvény, melynek értékkészlete a B halmaz. Az f függvény megfordítása (inverze) az a g függvény, amely minden B halmazbeli y elemhez azt az A halmazbeli x elemet rendeli, amelyre f (x) = y. Az f függvény megfordítását az f -1 szimbólummal jelölik. Például: 1. Legyen A = {kémiai elemek} és B = {vegyjelek}. Ekkor f : A → B minden elemhez a vegyjelét rendeli, például: vas ↦ Fe, ezüst ↦ Ag. A függvény megfordítása g : B → A, a vegyjelekhez az elemeket rendeli, például: S ↦ kén, Ra ↦ rádium. 2. Ha az f függvény minden valós számhoz a háromszorosát rendeli, akkor az f függvény megfordítása az a g függvény, amely minden valós számhoz a harmadrészét rendeli: f (x) = 3x, és g(x) = 1/3 x.
M	A függvény grafikonja	Ha az értelmezési tartomány és az értékkészlet is számhalmaz, akkor a függvény grafikonnal szemléltethető a derékszögű koordináta-rendszerben. Legyen az f függvénynek az x0 helyen felvett függvényértéke y0 (azaz y0 = f (x0)). Az egymáshoz tartozó x0 és y0 számokból alkotott (x0; y0) koordinátájú síkbeli pontok összessége adja a függvény grafikonját (másképp: a függvénygörbét).
D	Függvény zérushelye, szélsőértéke	Zérushely: az értelmezési tartomány azon x0 eleme (helye), amelyre f (x0) = 0, azaz ahol a függvényérték 0 (zérus). Maximum: az értékkészlet legnagyobb eleme, ha ez létezik. Maximumhely: az értelmezési tartomány azon eleme, amelyhez a maximum van hozzárendelve. Minimum: az értékkészlet legkisebb eleme, ha ez létezik. Minimumhely: az értelmezési tartomány azon eleme, amelyhez a minimum van hozzárendelve. Megjegyzés: Egy függvénynek lehet több zérushelye, maximumhelye, minimumhelye.
D	Monotonitás, a függvény menete (monoton növekvő; monoton csökkenő; szigorúan monoton növekvő; szigorúan monoton csökkenő)	Egy függvény az értelmezési tartományának egy adott intervallumán – monoton növekvő, ha az adott intervallum bármely két eleme közül a nagyobbikhoz legalább akkora helyettesítési érték tartozik, mint a kisebbikhez; – monoton csökkenő, ha az adott intervallum bármely két eleme közül a nagyobbikhoz legfeljebb akkora helyettesítési érték tartozik, mint a kisebbikhez; – szigorúan monoton növekvő, ha az adott intervallum bármely két eleme közül a nagyobbikhoz nagyobb helyettesítési érték tartozik, mint a kisebbikhez; – szigorúan monoton csökkenő, ha az adott intervallum bármely két eleme közül a nagyobbikhoz kisebb helyettesítési érték tartozik, mint a kisebbikhez. Például: Az f függvény a ]-6; 2] intervallumon monoton növekvő, ezen belül a ]-6; -2] intervallumon szigorúan monoton növekvő, a [-2; 2] intervallumon mondhatjuk monoton növekvőnek vagy monoton csökkenőnek is. Az f függvény a [2; 3[ intervallumon szigorúan monoton csökkenő. Ez teljesül a [2; 3[ intervallum részhalmazaira is, például a ]2; 3[ intervallumra is. A g függvény a ]-3; -1] intervallumon szigorúan monoton csökkenő. A g függvény a [-1; 8] intervallumon szigorúan monoton növekvő. Megjegyzés: A monotonitás értelmezhető akkor is, ha a függvény értelmezési tartománya nem intervallum, hanem más számhalmaz, például a természetes számok halmaza.
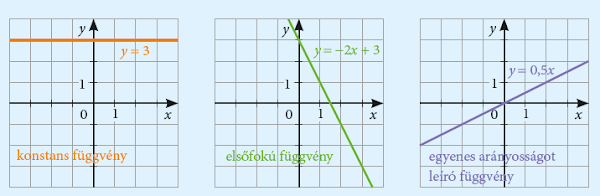
D	Lineáris függvény	Az f : R → R f (x) = ax + b (a, b ∈ R) függvényt lineáris függvénynek nevezzük. A függvény grafikonja egyenes, amelynek a meredeksége a, és az egyenes az y tengelyt a (0; b) pontban metszi. Ha a = 0, akkor f (x) = b konstans függvény (nulladfokú függvény); ha a ≠ 0, akkor f (x) = ax + b elsőfokú függvény; ha a ≠ 0 és b = 0, akkor f (x) = ax az a arányszámú egyenes arányosságot leíró függvény.
D	Fordított arányosságot leíró függvény	f : R \ {0} → R f(x) = a/x (a ∈ R; a ≠ 0) Az f(x) = 1/x függvény tulajdonságai: értékkészlet: R \ {0} zérushely nincs x < 0 esetén szigorúan monoton csökken 0 < x esetén szigorúan monoton csökken szélsőérték nincs
D	Abszolútérték-függvény	f : R → R f (x) = |x|, ahol , |x| = -x, ha x < 0 és |x| = x, ha 0 ≤ x. A függvény tulajdonságai: értékkészlet: R+0 zérushely: x0 = 0 x ≤ 0 esetén szigorúan monoton csökken 0 ≤ x esetén szigorúan monoton nő minimumhely: x = 0 minimum: y = 0
D	Másodfokú függvény alapfüggvény:	f : R → R f (x) = x² általános alak: f : R → R f (x) = ax² + bx + c (a, b, c ∈ R; a ≠ 0) Az alapfüggvény tulajdonságai: értékkészlet: R+0 zérushely: x0 = 0 x ≤ 0 esetén szigorúan monoton csökken 0 ≤ x esetén szigorúan monoton nő minimumhely: x = 0 minimum: y = 0
D	Négyzetgyökfüggvény	f : R0 + → R f (x) = √x A függvény tulajdonságai: értékkészlet: R+0 zérushely: x0 = 0 szigorúan monoton nő minimumhely: x = 0 minimum: y = 0
D	a alapú exponenciális függvény	f : R → R f(x) = ax (a ∈ R+, a ≠ 1) A függvény tulajdonságai: értékkészlet: R+ zérushely nincs szélsőérték nincs a monotonitás az a értékétől függ Ha a > 1, akkor a függvény szigorúan monoton nő, ha 0 < a < 1, akkor a függvény szigorúan monoton csökken.
M	Függvénytranszformáció	Egy f függvény görbéjének ismeretében újabb függvényeket tudunk ábrázolni függvénytranszformációk segítségével (a függvénytranszformációk hatása a függvény grafikonjára: eltolás, nyújtás vagy zsugorítás, tükrözés). Például:

KIDOLGOZOTT FELADAT

1. Az ábrán az f lineáris függvény grafikonján jelöltük a grafikonra illeszkedő A és B rácspontot.
Olvasd le az A és B pont koordinátáit, majd ezek segítségével határozd meg a függvény hozzárendelési szabályát!
Ennek ismeretében válaszolj az alábbiakra!
a) Milyen értéket vesz fel a függvény x = 123-nál?
b) Hol veszi fel a függvény az f (x) = 456 értéket?
c) Hol van a függvény zérushelye? A zérushely ismeretében oldd meg a valós számok halmazán az f (x) < 0 egyenlőtlenséget!

Megoldás

A pontok koordinátái: A(-5; 6) és B (5; -2), ez azt jelenti, hogy a függvény az x = -5 helyen 6, valamint az x = 5 helyen -2 értéket vesz fel.
A lineáris függvény képletét f(x) = ax + b alakban keressük.
Teljesül tehát a következő két egyenlőség:
6 = -5a + b és -2 = 5a + b.
Az a és b ismeretlenekre az egyenletrendszert megoldva kapjuk, hogy a = -0,8 és b = 2.
A lineáris függvény tehát az f (x) = -0,8x + 2 hozzárendelési szabállyal megadható.
a) x = 123 esetén a függvényérték helyettesítéssel számolható: f (123) = -0,8 ∙ 123 + 2, amiből f (123) = -96,4.
Tehát a függvényérték a keresett helyen -96,4.
b) Ha a függvényérték 456, akkor az x értéke a 456 = -0,8x + 2 egyenletből számítható.
Ebből x = -567,5, tehát a -567,5 helyen lesz a függvényérték 456.
c) A zérushely meghatározásakor azt a helyet kell meghatározni, ahol a függvényérték 0, ezért a 0 = -0,8x + 2 egyenlet megoldását keressük. Ebből x = 2,5 a függvény zérushelye.
A függvény szigorúan monoton csökkenő, ezért az f (x) 1 0 egyenlőtlenség megoldása – az ábráról is leolvasható – minden olyan valós x, amelyre 2,5 1 x.

---

2. Legyen f(x) = x² , valamint g az a függvény, amelynek grafikonja a koordináta-rendszerben az f függvény grafikonjának v(-3; -4) vektorral való eltolásával kapható meg.
a) Add meg a g függvény hozzárendelési szabályát!
b) Határozd meg mindkét függvény zérushelyét! Válaszod számolással indokold!
c) Add meg mindkét függvény szélsőértékeinek helyét és értékét!
d) Add meg a függvények értékkészletét!
e) Jellemezd a függvényeket monotonitás szempontjából!
f) Hol metszi a g függvény grafikonja a h(x) = -3 függvény grafikonját?
Válaszod számolással igazold!

Megoldás

a) Az f függvény v vektorral való eltolása után kapott g függvény grafikonja az ábrán látható.

A transzformáció alapján:
g : R → R g (x) = (x + 3)² - 4
b) A függvények zérushelye az ábráról leolvasva, majd számolással ellenőrizve:
az f függvény zérushelye x = 0, mert f (0) = 0^2 = 0; a g függvény zérushelye x_1 = -5, valamint x_2 = -1, mert g(-5) = (-5 + 3)² - 4 = 0, valamint g(-1) = (-1 + 3)² - 4 = 0.
c) Mindkét függvénynek van minimuma, egyiknek sincs maximuma.
Az f függvény minimumának helye x = 0, értéke f(0) = 0; a g függvény minimumának helye x = -3, értéke g(-3) = -4.
d) Az f függvény értékkészlete: Rf = [0; 3[; a g függvény értékkészlete: Rg = [-4; 3[
e) Az f függvény a ]-3; 0[ intervallumon szigorúan monoton csökkenő, a [0; 3[ intervallumon szigorúan monoton növekvő.
A függvény a ]-3; -3[ intervallumon szigorúan monoton csökkenő, a [-3; 3[ intervallumon szigorúan monoton növekvő.
f) Ábrázoljuk az előbbi koordináta-rendszerben a h függvényt is.
Az ábráról azt láthatjuk, hogy a g és h függvények grafikonjai metszéspontjainak első koordinátája vélhetően az x1 = -4, valamint x2 = -2.
Ezt számolással ellenőrizzük:
g(-4) = (-4 + 3)² - 4 = -3, valamint g(-2) = (-2 + 3)² - 4 = -3, azaz a felvett függvényérték az adott helyeken -3.
Tehát a g függvény grafikonja a h függvény grafikonját az x_1 = -4 és az x_2 = -2 helyeken metszi.

Megjegyzés:

A g és h függvény grafikonjainak metszéspontját meghatározhatjuk a g(x) = h(x), vagyis (x + 3)² - 4 = -3 másodfokú egyenlet megoldásával is.

---

3. a) Ábrázold az R \ {0} halmazon értelmezett f(x) = 1/x + 2 függvény grafikonját!
b) Ábrázold az R \ {0} halmazon értelmezett g = |f| függvény grafikonját!
c) Ábrázold az [1; 4] halmazon értelmezett h(x) = 1/x + 2 függvény grafikonját!
d) Határozd meg az f, g és h függvények értékkészletét!
e) Az f és a g függvény közül melyiknek van szélsőértéke? Határozd meg a szélsőértéket, illetve a szélsőértékhelyet!

Megoldás

a) Az f függvény grafikonját az R \ {0} halmazon értelmezett x ↦ 1/x függvény transzformációjával kapjuk úgy, hogy ez utóbbit eltoljuk a v(0; 2) vektorral.

b) A g függvény grafikonját az f függvény grafikonjából úgy kapjuk, hogy a grafikonnak azt a részét, amelyik az x tengely „alá” esik, tükrözzük az x tengelyre.

c) A h függvény grafikonját az f függvény grafikonjából úgy kapjuk, hogy a grafikonnak azt a részét jelöljük ki, amelyik az 1 ≤ x ≤ 4 helyekhez tartozik.

d) A grafikonok alapján meghatározhatjuk a függvények értékkészletét.
A h függvény esetében behelyettesítéssel tudjuk kiszámolni, hogy x = 1 és x = 4 helyen mennyi a függvényérték: h(1) = 1/1 + 2 = 3, és h(4) = 1/4 + 2 = 2,25.
Rf = R \ {2} Rg = R0 + Rh = [2,25; 3]
e) A grafikonról leolvasható, hogy f függvénynek nincs szélsőértéke.
A g függvénynek maximuma nincs, de minimuma van azon a helyen, ahol a függvényérték 0.
0 = 1/x + 2, ebből 1/x =-2, így x =- 1/2 .
A minimumhely tehát az x =- 1/2 , a minimuma pedig y = 0.

FELADATOK I. RÉSZ

A1. Függvény vagy sem? Kölcsönösen egyértelmű vagy sem?
A táblázat minden sorában tegyél X-et abba az oszlopba, amelyik teljesül az adott hozzárendelés esetében!

	Nem függvény	Függvény, de nem kölcsönösen egyértelmű	Kölcsönösen egyértelmű függvény
Minden valós számhoz hozzárendeljük a négyzetét.
Minden háromszöghöz hozzárendeljük azt a pozitív valós számot, amely megadja területének nagyságát cm2-ben mérve.
Minden egész számhoz hozzárendeljük azt a valós számot, amelytől 2 egység távolságra van a számegyenesen.
Minden valós számhoz hozzárendeljük a hozzá legközelebb eső egész számot.
Minden valós számhoz hozzárendeljük a számnál 5-tel nagyobb számot.

---

A2. Határozd meg a valós számok halmazán értelmezett f (x) = 2x² - x - 1 függvény zérushelyeit!

---

A3. Add meg annak a lineáris függvénynek a hozzárendelési szabályát, amelynek grafikonjára illeszkedik az A(-3; 2), valamint a B(5; 4) koordinátájú pont!

---

A4. Mennyi a helyettesítési értéke az x = 2- 1 helyen a valós számokon értelmezett f (x) = 9x + 5 függvénynek?

---

A5. a) Válaszd ki az ábrán lévő grafikonhoz a megfelelő hozzárendelési szabály betűjelét!
A: f (x) = (x + 5)² - 2
B: f (x) = (x - 2)² - 5
C: f (x) = (x + 2)² - 5
D: f (x) = (x - 2)² + 5
E: f (x) = x² - 2x + 5
F: f (x) = (x + 5)² + 2

b) Add meg azt a legbővebb intervallumot, ahol negatív az a) feladatrészben ábrázolt f függvény értéke!

---

A6. Számítsd ki a valós számok halmazán értelmezett f (x) = 0,5^x - 8 függvény zérushelyét!

---

A7. Döntsd el az alábbi állítások mindegyikéről, hogy igaz-e, vagy hamis!
A: Minden, a valós számok halmazán értelmezett másodfokú függvénynek van szélsőértéke.
B: Minden hozzárendelés függvény.
C: Minden elsőfokú függvény menete szigorúan monoton.
D: Van olyan exponenciális függvény, amelynek van zérushelye.

---

A8. Jellemezd a valós számok halmazán értelmezett f (x) = -7/3 x + 22 függvényt monotonitás szempontjából!

---

A9. Hol veszi fel a valós számokon értelmezett f (x) = -7x + 16 függvény a 13 értéket?

---

A10. Hány olyan függvény van, amelynek értelmezési tartománya az A = {1; 2; 3} halmaz, és értékkészlete a B = {5; 6; 7} halmaz?
Ezek közül hány függvény kölcsönösen egyértelmű?

---

A11. Add meg képlet segítségével az alábbi függvényeket!
f: Minden valós számhoz hozzárendeljük az 5-szörösénél 2-vel kisebb számot.
g: Minden valós számhoz hozzárendeljük a számnál 4-gyel nagyobb szám négyzetét.
h: Minden valós számhoz hozzárendeljük az abszolút értékének az ellentettjét.
i: Minden valós számhoz hozzárendeljük a négyzetgyökénél 6-tal nagyobb számot.

---

A12. Az ábrán egy f függvény grafikonja látható.
Add meg az |f| függvény

a) minimumát és minimumhelyeit!
b) maximumát és maximumhelyét!

FELADATOK II. RÉSZ

P1. Az ábrán egy ferdén kilőtt, parabolapályán haladó test mozgását jelenítettük meg.

A kilövés az időmérés kezdetén (x = 0 s) történt a talajszintnél magasabban lévő helyről.
Az x tengelyen az eltelt időt (1 másodperc 1 egység), az y tengelyen a test talajtól mért magasságát (1 méter 1 egység) mérjük.
A pályagörbét leíró függvény f (x) = -(x - 2)² + 9.
a) Igazold, hogy a test a kilövéskor 5 méter magasan volt!
b) A kilövéstől számítva mennyi idő múlva éri el a test a pálya legmagasabb pontját?
Milyen távol van ekkor a talajtól?
c) A kilövéstől számítva hány másodperc múlva lesz a test 8 méter magasan?
d) A kilövéstől számítva hány másodperc múlva érkezik a talajra a test?

---

P2. Az f és a g függvény értelmezési tartománya az R, f(x) = 3 - 2x ; g(x) = x² .
a) Ábrázold közös koordináta-rendszerben az f és a g függvény grafikonját!
b) Olvasd le az ábrádról, mely x-ekre teljesül az f(x) = g(x) egyenlet!
c) Ellenőrizd a b) részben kapott eredményt a másodfokú egyenlet megoldóképletével!
d) Oldd meg grafikusan az f (x) > g(x) egyenlőtlenséget!

---

P3. Egy internetes csomagküldő szolgálatnál a csomagküldés díja egy fix csomagolási díjból és a csomag tömegével egyenesen arányos szállítási díjból tevődik össze.
Az x dekagramm tömegű csomagért (forintban) fizetendő díjat az f (x) = 12x + 640 képlettel számítják ki.
Ha a csomag tömege eléri a 10 kg-ot, akkor az f (x) = 12x + 640 összegen felül csomagonként további 1100 Ft extra költséget számít fel a cég.
25 kg-nál nehezebb csomag kiszállítását nem vállalják.
a) Mennyi a fix csomagolási díj?
b) Mennyi az 1 dkg-ra jutó szállítási díj egy 10 kg-nál könnyebb csomag esetén?
c) Mennyibe kerül egy 450 grammos csomag küldése?
d) Hány kilogramm annak a küldeménynek a tömege, amiért összesen 1600 forintot kell fizetni?
e) Készíts grafikont a csomagokért fizetendő díjról a csomag tömegének függvényében!
f) Milyen határok között mozoghat a csomagokért fizetendő díj?

---

P4. Megadtuk hat függvény hozzárendelési szabályát és közülük háromnak a grafikonját.
A függvények értelmezési tartománya a valós számok halmaza.
p: x ↦ 0,5|x + 2|
q: x ↦ -2|x|
r: x ↦ |x - 2|
s: x ↦ |x + 2|
t: x ↦ -0,5|x|
u: x ↦ 0,5|x -2|

a) Válaszd ki az adottak közül az ábrán lévő három grafikonhoz tartozó hozzárendelési szabályokat!
b) Határozd meg az ábrán lévő függvények 0-hoz rendelt értékét!
c) Add meg az ábrán lévő függvények zérushelyeit!
d) Jellemezd az ábrán lévő függvényeket szélsőértékek szempontjából!

---

P5. Arnd Leike német fizikus – aki a müncheni Ludwig Maximilian Egyetem fizika tanszékének munkatársa, és alapvetően a részecskefizika a fő kutatási területe – a sörhab magasságának változására vonatkozó vizsgálatot végzett a 2000-es évek elején.
Háromféle 19 °C-os hőmérsékletű sörrel kísérletezett.
A sört az üvegből egy 7,2 cm átmérőjű hengerbe töltötte.
A sörhab néhány másodperc alatt elérte maximális magasságát, majd kezdett fokozatosan leapadni.
Leike 15 másodpercenként mérte meg a sörhab magasságát.
Az egyik sör esetében azt tapasztalta, hogy a sörhab mm-ben mért magasságának változását jó közelítéssel az f (t) = 14 ∙ 0,991^t függvény írja le a [0, 360] időintervallumban az eltelt t (másodpercekben mért) idő függvényében.
a) Hány mm magas volt eredetileg ennek a sörnek a habja?
b) Milyen magas volt a hab 1 perc eltelte után?
c) Hány másodperc elteltével volt a hab magassága 3 mm?
A válaszod egy tizedesjegy pontossággal add meg!
d) Vázold a hab magasságára vonatkozó függvény grafikonját a derékszögű koordináta-rendszerben az első 120 s-ra vonatkozóan!
Válaszd meg észszerűen a koordinátatengelyek beosztását!
(A sörhabbal kapcsolatos tanulmányért Leike doktor később – a hasonló nevű Nobel-díjtól eltérő – Ignobel-díjat kapott, amit a meglepő, ám haszontalan felfedezésekért ítélnek oda.)